Contenido
INTRODUCCIÓN
3.1. MATRICES
3.1.1. OPERACIONES CON MATRICES
3.2. VECTORES
3.3. ELIMINACIÓN DE GAUSS
3.4. ELIMINACIÓN DE GAUSS-JORDAN
3.5. ESTRATEGIAS DE PIVOTEO
3.6. MÉTODO DE CHOLESKY
3.7. MÉTODO DE DESCOMPOSICIÓN LU
3.8. MÉTODO DE GAUSS-SEIDEL
3.9. MÉTODO ITERATIVO
3.3. ELIMINACIÓN DE GAUSS
3.4. ELIMINACIÓN DE GAUSS-JORDAN
3.5. ESTRATEGIAS DE PIVOTEO
3.6. MÉTODO DE CHOLESKY
3.7. MÉTODO DE DESCOMPOSICIÓN LU
3.8. MÉTODO DE GAUSS-SEIDEL
3.9. MÉTODO ITERATIVO
3.9.1. MÉTODO JACOBI
BIBLIOGRAFIAEn esta unidad se abordaran temas como el de los sistemas de ecuaciones lineales, las matrices, la suma de vectores y entre otros temas.
3.1. MATRICES
Una matriz es un conjunto de números reales, que están dispuestos en “m” filas y en “n” columnas:
A los números que forman la matriz se les llama elementos.
El número de filas por el número de columnas se denomina dimensión de la matriz y se designa como m x n, siendo m el número de filas y n el número de columnas.
Por ejemplo, estas son matrices de diferentes dimensiones:
Donde la matriz A es una matriz de 2×3 (2 filas y 3 columnas), la matriz B es una matriz de 3×2 (3 filas y 2 columnas) y la matriz C es una matriz de 3×3 (3 filas y 3 columnas).
A continuación vamos a ver los tipos de matrices que existen, junto con un ejemplo de cada una de ellas.
Matriz rectangular
Es aquella que tiene distinto número de filas que de columnas (m≠n):
Matriz fila
Es toda matriz rectangular que tiene una sola fila (m = 1).
Matriz columna
Es toda matriz rectangular con una columna (n = 1).
Matriz opuesta
La matriz opuesta a otra matriz es la que tiene todos los elementos de signo contrario a la matriz original. Por ejemplo, si tenemos la matriz A:
La matriz opuesta a A se designa como -A, donde que todos los elementos son de signo contrario a los elementos de la matriz A.
Matriz traspuesta
Se llama matriz traspuesta de una matriz cualquiera de dimensión m x n a la matriz que se obtiene al convertir las filas en columnas. Se representa con el súper-índice “t” y su dimensión es por tanto n x m.
Por ejemplo, tenemos la siguiente matriz A, de dimensión 2 x 3 (2 filas y 3 columnas):
Su matriz traspuesta, designada con el súper-índice “t”, se obtiene convirtiendo las filas en columnas. Por tanto, la primera fila de la matriz A, formada por los elementos 1, -3 y 0, pasa a ser la primera columna de su matriz traspuesta. De la misma forma, la segunda fila de la matriz A, formada por los elementos 2, 4 y 1, pasa a ser la segunda columna de su matriz traspuesta:
La dimensión de la matriz traspuesta de A es de 3 x 2 (3 filas y 2 columnas):
Matriz cuadrada de orden n
Una matriz cuadrada es aquella que tiene igual número de filas que de columnas (m = n). En este caso, la dimensión se denomina orden, cuyo valor coincide con el número de filas y de columnas.
Por ejemplo, la siguiente matriz es una matriz cuadrada de orden 3, ya que tiene 3 filas y 3 columnas:
Entre los elementos de las matrices cuadradas suelen tenerse muy en cuenta los que forman las diagonales de la matriz.
Así, se llama diagonal principal de una matriz cuadrada a los elementos que componen la diagonal que va desde la esquina superior izquierda, hasta la esquina inferior derecha:
Así, se llama diagonal principal de una matriz cuadrada a los elementos que componen la diagonal que va desde la esquina superior izquierda, hasta la esquina inferior derecha:
Se llama diagonal secundaria de una matriz cuadrada a los elementos que componen la diagonal que va desde la esquina superior derecha, hasta la esquina inferior izquierda:
Matriz triangular superior
Es toda matriz cuadrada donde al menos uno de los términos que están por encima de la diagonal principal son distintos de cero y todos los términos situados por debajo de la diagonal principal son ceros:
Normalmente, cuando se dice que hay que triangular la matriz, se refiere a que hay que hacer ceros los elementos que quedan por debajo de la diagonal principal.
Matriz triangular inferior
Es toda matriz cuadrada donde al menos uno de los términos que están por debajo de la diagonal principal son distintos de cero y todos los términos situados por encima de la diagonal principal son ceros:
Matriz diagonal
Es toda matriz cuadrada en la que todos los elementos que no están situados en la diagonal principal son ceros:
Matriz escalar
La matriz escalar es toda matriz diagonal donde todos los elementos de la diagonal principal son iguales:
Matriz identidad
Es la matriz escalar cuyos elementos de la diagonal principal valen uno, es decir, la diagonal principal está formada por 1, y el resto de los elementos son 0:
Matriz nula
La matriz nula donde todos los elementos son cero. Suele designarse con un 0:
3.1.1. OPERACIONES CON MATRICES
Suma de matrices
Dadas dos o más matrices del mismo orden, el resultado de la suma es otra matriz del mismo orden cuyos elementos se obtienen como suma de los elementos colocados en el mismo lugar de las matrices sumandos.
Ejemplo:
Resta de matrices
Dadas dos o más matrices del mismo orden, el resultado de la resta es otra matriz del mismo orden cuyos elementos se obtienen como la resta de los elementos colocados en el mismo lugar de las matrices sumandos.
Ejemplo:
Multiplicación por un número
Para multiplicar una matriz cualquiera por un número real, se multiplican todos los elementos de la matriz por dicho número.
Ejemplo:
Producto de matrices
El resultado de multiplicar dos matrices es otra matriz en la que el elemento que ocupa el lugar cij se obtiene sumando los productos parciales que se obtienen al multiplicar todos los elementos de la fila “i” de la primera matriz por los elementos de la columna “j” de la segunda matriz.
Es decir, multiplicamos la primera fila por los elementos de la primera columna y el resultado será nuestro nuevo elemento. Para ello, el número de columnas de la primera matriz debe coincidir con el de filas de la segunda. Si no fuese así no podríamos realizar la operación.
Ejemplo:
Observamos como la matriz resultante tiene el número de filas de la primera y el de columnas de la segunda.
Debemos recordar, que las matrices no tienen la propiedad conmutativa. En el caso de que se pudiera operar A.B y B.A el resultado por lo general puede ser diferente.
3.2. VECTORES
Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son:
Origen
O también denominado Punto de aplicación. Es el punto exacto sobre el que actúa el vector.
Módulo
Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo.
Dirección
Viene dada por la orientación en el espacio de la recta que lo contiene.
Sentido
Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.
Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial. Podemos considerarlo como un segmento orientado, en el que cabe distinguir:
Un origen o punto de aplicación: A.
Un extremo: B.
Una dirección: la de la recta que lo contiene.
Un sentido: indicado por la punta de flecha en B.
Un módulo, indicativo de la longitud del segmento AB.
Suma y resta de vectores
Para sumar dos vectores libres
y 
se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.
Regla del paralelogramo
Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.
Para sumar dos vectores se suman sus respectivas componentes.
Propiedades de la suma de vectores
1 Asociativa
+ ( + 
) = ( + ) +
2 Conmutativa
+ = +
3 Elemento neutro
+ 
=
4 Elemento opuesto
+ (− ) =
1 Asociativa
+ ( + ) = ( + ) + 2 Conmutativa
+ = + 3 Elemento neutro
+ = 4 Elemento opuesto
+ (− ) = Resta de vectores
Para restar dos vectores libres y se suma con el opuesto de .
Las componentes del vector resta se obtienen restando las componentes de los vectores.
y se suma con el opuesto de . Las componentes del vector resta se obtienen restando las componentes de los vectores.
3.3. ELIMINACIÓN DE GAUSS
En el primer paso, multiplicamos la primera ecuación por
y la restamos a la segunda, después multiplicamos la
primera ecuación por
y la restamos a la
tercera y finalmente multiplicamos la primera ecuación por
y la restamos a la cuarta. Los números 2,
y -1 son los multiplicadores del primer paso
del proceso de eliminación. El número 6 es el elemento
pivote de este primer paso y la primera fila, que no sufre
modificación alguna, se denomina fila pivote. El sistema en
estos momentos tiene el siguiente aspecto: 
En el siguiente paso del proceso, la segunda fila se emplea como fila pivote y -4 como elemento pivote.
Aplicamos del nuevo el proceso: multiplicamos la segunda fila por
y la restamos de la tercera y después multiplicamos
la segunda fila por
y la restamos a la
cuarta. Los multiplicadores son en esta ocasión 3 y
y
el sistema de ecuaciones se reduce a: 
El último paso consiste en multiplicar la tercera ecuación por
y restarla a la cuarta. El sistema resultante resulta
ser: 
El sistema resultante es triangular superior y equivalente al sistema original (las soluciones de ambos sistemas coinciden). Sin embargo, este sistema es fácilmente resoluble aplicando el algoritmo de sustitución regresiva.
La solución del sistema de ecuaciones resulta ser:
Si colocamos los multiplicadores utilizados al transformar el sistema en una matriz triangular inferior unitaria (L) ocupando cada uno de ellos la posición del cero que contribuyó a producir, obtenemos la siguiente matriz:
Por otra parte, la matriz triangular superior (U) formada por los coeficientes resultantes tras aplicar el algoritmo de Gauss, es:
Estas dos matrices nos dan la factorización LU de la matriz inicial de coeficientes, A
3.4. ELIMINACIÓN DE GAUSS-JORDAN
El método consiste en aplicar operaciones elementales fila, es decir, cualquier fila se puede multiplicar por cualquier número (distinto de cero) o se le puede sumar o restar cualquier otra fila multiplicada o no por cualquier número. No se puede restar una fila a ella misma. También puede intercambiarse el orden de las filas (por ejemplo, intercambiar las dos primera filas).
El proceso debe aplicarse hasta que se obtenga la matriz en forma escalonada (método de Gauss) o en forma escalonada reducida (método Gauss-Jordan) de la matriz ampliada.
Recordamos que una matriz en su forma escalonada reducida cumple:
En cada fila, el primer elemento distinto de cero (de izquierda a derecha) es un 1 (uno principal). A la izquierda de este 1, sólo hay ceros. A su derecha puede haber cualquier número. En la columna del 1 principal de las filas de arriba y las de abajo sólo puede haber ceros (a no ser que sea la primera fila y por encima del 1 no hay ningún elemento).
El uno principal de cualquier fila se sitúa más a la izquierda de los unos principales de las filas inferiores a ésta.
Si existen filas formadas únicamente por ceros, éstas son las inferiores.
Ejemplos
Multiplicamos la primera fila por 1/5 y la segunda por 1/3
Sumamos a la segunda fila la primera
Es decir, hemos obtenido la solución del sistema.
3.5. ESTRATEGIAS DE PIVOTEO
Los algoritmos de Gauss y Gauss-Jordan que acabamos de describir pueden dar lugar a resultados erróneos fácilmente. Por ejemplo, analicemos el siguiente sistema de ecuaciones, en el que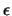 
es un número muy pequeño pero distinto de cero:
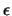es un número muy pequeño pero distinto de cero: 
Al aplicar el algoritmo gaussiano se obtiene el siguiente sistema
triangular superior:
y la solución es:
En una computadora, si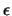
es suficientemente pequeño, los
términos
y
se procesaran como un
mismo número, por lo que
y
.
Sin
embargo, la solución correcta es:
es suficientemente pequeño, los
términos
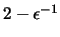y
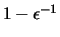se procesaran como un
mismo número, por lo que
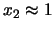y
.
Sin
embargo, la solución correcta es: 
Tenemos entonces que la solución calculada es exacta para x2 pero
extremadamente inexacta para x1.
La conclusión que podemos extraer es que un buen algoritmo debe incluir el intercambio de ecuaciones cuando las circunstancias así lo exijan.
Un algoritmo que cumple este requisito es el denominado eliminación gaussiana con pivoteo de filas escaladas.
3.6. MÉTODO DE CHOLESKY
En general, si A es Hermitiana y definida positiva, entonces A puede ser descompuesta como A = LL*
donde L es una matriz triangular inferior con entradas diagonales estrictamente positivas y L* representa la conjugada traspuesta de L. Esta es la descomposición de Cholesky.
La descomposición de Cholesky es única: dada una matriz Hermitiana positiva definida A, hay una única matriz triangular inferior L con entradas diagonales estrictamente positivas tales que A = LL*.
El recíproco se tiene trivialmente: si A se puede escribir como LL* para alguna matriz invertible L, triangular inferior o no, entonces A es Hermitiana y definida positiva.
El requisito de que L tenga entradas diagonales estrictamente positivas puede extenderse para el caso de la descomposición en el caso de ser semidefinida positiva. La proposición se lee ahora: una matriz cuadrada A tiene una descomposición de Cholesky si y sólo si A es Hermitiana y semide-finida positiva. Las factorizaciones de Cholesky para matrices semi-definidas positivas no son únicas en general.
3.7. MÉTODO DE DESCOMPOSICIÓN LU
El paso de la eliminación que consume tiempo se puede reformular de tal manera que involucre sólo operaciones sobre los coeficientes de [A].
Conveniente para situaciones donde se tienen que evaluar varias veces el vector [b], para un mismo valor de [A].
El método de eliminación de Gauss se puede implementar como una descomposición LU.
LU proporciona un medio eficiente para calcular la matriz inversa.
Revisión de descomposición LU:
La anterior es una estrategia de dos pasos:
Descomposición LU: La matriz a se factoriza o "descompone" en matrices triangular inferior (L), y superior (U).
Sustitución: L y U se usan para determinar una solución x para un lado derecho b. Este a su vez se divide en dos:
– Ld = b, se usa para generar un vector intermedio d por sustitución hacia delante.
– El resultado es sustituido en Ux – d = 0, que se resuelve por sustitución hacia atrás.
Complejidad de resolver Sistemas Lineales usando el método LU:
La eliminación Gaussiana para realizar la descomposición LU presenta un costo computacional del orden de m3/3.
Se puede resolver un sistema lineal explícitamente invirtiendo la matriz, entonces la solución es dada por: x = A-1b.
Calcular A-1 es tan costoso como resolver el sistema mismo.
La inversión explícita es 3 veces más costosa como la descomposición LU.
Produce pérdida de precisión en la respuesta.
3.8. MÉTODO DE GAUSS-SEIDEL
El método de eliminación para resolver ecuaciones simultáneas suministra soluciones suficientemente precisas hasta para 15 o 20 ecuaciones. El número exacto depende de las ecuaciones de que se trate, del número de dígitos que se conservan en el resultado de las operaciones aritméticas, y del procedimiento de redondeo. Utilizando ecuaciones de error, el número de ecuaciones que se pueden manejar se puede incrementar considerablemente a más de 15 o 20, pero este método también es impráctico cuando se presentan, por ejemplo, cientos de ecuaciones que se deben resolver simultáneamente. El método de inversión de matrices tiene limitaciones similares cuando se trabaja con números muy grandes de ecuaciones simultáneas.
Sin embargo, existen varias técnicas que se pueden utilizar, para resolver grandes números de ecuaciones simultáneas. Una de las técnicas más útiles es el método de Gauss-Seidel. Ninguno de los procedimientos alternos es totalmente satisfactorio, y el método de Gauss-Seidel tiene la desventaja de que no siempre converge a una solución o de que a veces converge muy lentamente. Sin embargo, este método convergirá siempre a una solución cuando la magnitud del coeficiente de una incógnita diferente en cada ecuación del conjunto, sea suficientemente dominante con respecto a las magnitudes de los otros coeficientes de esa ecuación.
Es difícil definir el margen mínimo por el que ese coeficiente debe dominar a los otros para asegurar la convergencia y es aún más difícil predecir la velocidad de la convergencia para alguna combinación de valores de los coeficientes cuando esa convergencia existe. No obstante, cuando el valor absoluto del coeficiente dominante para una incógnita diferente para cada ecuación es mayor que la suma de los valores absolutos de los otros coeficientes de esa ecuación, la convergencia está asegurada. Ese conjunto de ecuaciones simultáneas lineales se conoce como sistema diagonal.
Un sistema diagonal es condición suficiente para asegurar la convergencia pero no es condición necesaria. Afortunadamente, las ecuaciones simultáneas lineales que se derivan de muchos problemas de ingeniería, son del tipo en el cual existen siempre coeficientes dominantes.
La secuencia de pasos que constituyen el método de Gauss-Seidel es la siguiente:
Sin embargo, existen varias técnicas que se pueden utilizar, para resolver grandes números de ecuaciones simultáneas. Una de las técnicas más útiles es el método de Gauss-Seidel. Ninguno de los procedimientos alternos es totalmente satisfactorio, y el método de Gauss-Seidel tiene la desventaja de que no siempre converge a una solución o de que a veces converge muy lentamente. Sin embargo, este método convergirá siempre a una solución cuando la magnitud del coeficiente de una incógnita diferente en cada ecuación del conjunto, sea suficientemente dominante con respecto a las magnitudes de los otros coeficientes de esa ecuación.
Es difícil definir el margen mínimo por el que ese coeficiente debe dominar a los otros para asegurar la convergencia y es aún más difícil predecir la velocidad de la convergencia para alguna combinación de valores de los coeficientes cuando esa convergencia existe. No obstante, cuando el valor absoluto del coeficiente dominante para una incógnita diferente para cada ecuación es mayor que la suma de los valores absolutos de los otros coeficientes de esa ecuación, la convergencia está asegurada. Ese conjunto de ecuaciones simultáneas lineales se conoce como sistema diagonal.
Un sistema diagonal es condición suficiente para asegurar la convergencia pero no es condición necesaria. Afortunadamente, las ecuaciones simultáneas lineales que se derivan de muchos problemas de ingeniería, son del tipo en el cual existen siempre coeficientes dominantes.
La secuencia de pasos que constituyen el método de Gauss-Seidel es la siguiente:
1. Asignar un valor inicial a cada incógnita que aparezca en el conjunto. Si es posible hacer una hipótesis razonable de éstos valores, hacerla. Si no, se pueden asignar valores seleccionados arbitrariamente. Los valores iniciales utilizados no afectarán la convergencia como tal, pero afectarán el número de iteraciones requeridas para dicha convergencia.
2. Partiendo de la primera ecuación, determinar un nuevo valor para la incógnita que tiene el coeficiente más grande en esa ecuación, utilizando para las otras incógnitas los valores supuestos.
3. Pasar a la segunda ecuación y determinar en ella el valor de la incógnita que tiene el coeficiente más grande en esa ecuación, utilizando el valor calculado para la incógnita del paso 2 y los valores supuestos para las incógnitas restantes.
4. Continuar con las ecuaciones restantes, determinando siempre el valor calculado de la incógnita que tiene el coeficniente más grande en cada ecuación particular, y utilizando siempre los últimos valores calculados para las otras incógnitas de la ecuación. (Durante la primera iteración, se deben utilizar los valores supuestos para las incógnitas hasta que se obtenga un valor calculado). Cuando la ecuación final ha sido resuelta, proporcionando un valor para la única incógnita, se dice que se ha completado una iteración.
5. Continuar iterando hasta que el valor de cada incógnita, determinado en una iteración particular, difiera del valor obtenido en la iteración previa, en una cantidad menor que cierto
seleccionado arbitrariamente. El procedimiento queda entonces completo.
Refiriéndonos al paso 5, mientras menor sea la magnitud del
seleccionado, mayor será la precisión de la solución. Sin embargo, la magnitud del epsilon no especifica el error que puede existir en los valores obtenidos para las incógnitas, ya que ésta es una función de la velocidad de convergencia. Mientras mayor sea la velocidad de convergencia, mayor será la precisión obtenida en los valores de las incógnitas para un
dado.
EJEMPLO
Resolver el siguiente sistema de ecuación por el método Gauss-Seidel utilizando un
= 0.001.
SOLUCIÓN:
Primero ordenamos las ecuaciones, de modo que en la diagonal principal estén los coeficientes mayores para asegurar la convergencia.
Primero ordenamos las ecuaciones, de modo que en la diagonal principal estén los coeficientes mayores para asegurar la convergencia.
Despejamos cada una de las variables sobre la diagonal:
La primera iteración se completa sustituyendo los valores de X1 y X2 calculados obteniendo:
Comparando los valores calculados entre la primera y la segunda iteración
Como podemos observar, no se cumple la condición
Entonces tomamos los valores calculados en la última iteración y se toman como supuestos para la siguiente iteración. Se repite entonces el proceso:
Como se observa todavía no se cumple la condición
Así que hacemos otra iteración
Dado que se cumple la condición, el resultado es:
| X1 = 3.0 |
| X2 = -2.5 |
| X3 = 7.0 |
Como se puede comprobar no se tiene un número exacto de
iteraciones para encontrar una solución. En este ejemplo, se
hicieron 3 iteraciones, pero a menudo se necesitan más iteraciones.
3.9. MÉTODO ITERATIVO
Un método iterativo trata de resolver un problema matemático (como una ecuación o un sistema de ecuaciones) mediante aproximaciones sucesivas a la solución, empezando desde una estimación inicial. Esta aproximación contrasta con los métodos directos, que tratan de resolver el problema de una sola vez (como resolver un sistema de ecuaciones Ax=b encontrando la inversa de la matriz A). Los métodos iterativos son útiles para resolver problemas que involucran un número grande de variables (a veces del orden de millones), donde los métodos directos tendrían un coste prohibitivo incluso con la potencia del mejor computador disponible.
En el caso de un sistema lineal de ecuaciones, las dos clases principales de métodos iterativos son los métodos iterativos estacionarios y los más generales métodos del sub-espacio de Krylov
Métodos iterativos estacionarios
Los métodos iterativos estacionarios resuelven un sistema lineal con un operador que se aproxima al original, y basándose en la medida de error (el residuo), desde unaecuación de corrección para la que se repite este proceso. Mientras que estos métodos son sencillos de derivar, implementar y analizar, la convergencia normalmente sólo está garantizada para una clase limitada de matrices.
Métodos del subespacio de Krylov
Los métodos del sub-espacio de Krylov forman una base ortogonal de la secuencia de potencias de la matriz por el residuo inicial (la secuencia de Krylov). Las aproximaciones a la solución se forman minimizando el residuo en el sub-espacio formado. El método prototípico de esta clase es el método de gradiente conjugado. Otros métodos son el método del residuo mínimo generalizado y el método del gradiente bi-conjugado.
Convergencia
Dado que estos métodos forman una base, el método converge en N iteraciones, donde N es el tamaño del sistema. Sin embargo, en la presencia de errores de redondeo esta afirmación no se sostiene; además, en la práctica N puede ser muy grande, y el proceso iterativo alcanza una precisión suficiente mucho antes. El análisis de estos métodos es difícil, dependiendo de lo complicada que sea la función del espectro del operador.
Pre-condicionantes
El operador aproximativo que aparece en los métodos iterativos estacionarios puede incorporarse también en los métodos del sub-espacio de Krylov, donde se pasan de ser transformaciones del operador original a un operador mejor condicionado. La construcción de pre-condicionadores es un área de investigación muy extensa y de gran alcance científico.
3.9.1. MÉTODO JACOBI
En la iteración de Jacobi, se escoge una matriz Q que es diagonal y cuyos elementos diagonales son los mismos que los de la matriz A. La matriz Q toma la forma:
y la ecuación general se puede escribir como
Qx(k) = (Q-A)x(k-1) + b
Si denominamos R a la matriz A-Q:
la ecuación se puede reescribir como:
Qx(k) = -Rx(k-1) + b
El producto de la matriz Q por el vector columna x(k) será un
vector columna. De modo análogo, el producto de la matriz R por el
vector columna x(k-1) será también un vector columna.
La expresión
anterior, que es una ecuación vectorial, se puede expresar por n ecuaciones escalares (una para cada componente del vector). De este
modo, podemos escribir, para un elemento i cualquiera y teniendo en
cuenta que se trata de un producto matriz-vector:
Si tenemos en cuenta que en la matriz Q todos los elementos fuera de
la diagonal son cero, en el primer miembro el único término no nulo
del sumatorio es el que contiene el elemento diagonal qii, que es
precisamente aii.
Más aún, los elementos de la diagonal de R son cero, por lo que podemos eliminar el término i=j en el sumatorio
del segundo miembro. De acuerdo con lo dicho, la expresión anterior se
puede reescribir como:
de donde despejando xi(k) obtenemos:
que es la expresión que nos proporciona las nuevas componentes del
vector x(k) en función de vector anterior x(k-1) en la
iteración de Jacobi.
El método de Jacobi se basa en escribir el sistema de ecuaciones en la
forma:
Partimos de una aproximación inicial para las soluciones al sistema de
ecuaciones y sustituimos estos valores en la
ecuación.
De esta forma, se genera una nueva
aproximación a la solución del sistema, que en determinadas
condiciones, es mejor que la aproximación inicial.
Esta nueva
aproximación se puede sustituir de nuevo en la parte derecha de la
ecuación y así sucesivamente hasta obtener la
convergencia.
BIBLIOGRAFÍA
Apuntes de la clase de métodos numéricos por la Mtra. Lorena Alonso Guzmán.
https://www.uv.es/~diaz/mn/fmn.html
http://aniei.org.mx/paginas/uam/CursoMN/index.html
http://aprendeenlinea.udea.edu.co/lms/moodle/course/view.php?id=229
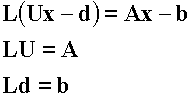
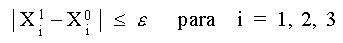
No hay comentarios.:
Publicar un comentario