Contenido
- Introducción
- Método de Newton-Cotes
- Método Trapezoidal
- Método Trapezoidal compuesto
- Método de Simpson 1/3
- Método de Simpson 3/8
- Cuadratura de Gauss
- Diferenciación Numérica
- Bibliografía
La integración numérica constituye una amplia gama de algoritmos para calcular el valor numérico de una integral definida y, por extensión, el término se usa a veces para describir algoritmos numéricos para resolver ecuaciones diferenciales.
Método de Newton-Cotes
Las fórmulas de Newton - Cotes son los tipos de integración numérica más comunes. Se basan en la estrategia de reemplazar una función complicada o datos tabulados por un polinomio de aproximación que es fácil de integrar:
donde fn(x) es un polinomio de la forma
donde n es el grado del polinomio. Por ejemplo, en la Figura 1 se utiliza un polinomio de primer grado como una aproximación, mientras que en la Figura 2, se emplea una parábola con el mismo propósito.
La integral también se puede aproximar usando un conjunto de polinomios aplicados por pedazos a la función o datos, sobre segmentos de longitud constante. Así, en la Figura 3, se usan tres segmentos de línea recta para aproximar la integral.
El grado de precisión de una fórmula de integración numérica es el número natural n que verifica que el error de truncamiento E[Pi]=0 para todos los polinomios Pi(x) de grado i ≤ n, y existe un polinomio Pn+1(x) de grado n+1 tal que E[Pn+1]≠0.
Método Trapezoidal
La regla del trapecio es la primera de las fórmulas cerradas de Newton - Cotes. Corresponde al caso donde el polinomio de aproximación es de primer grado:
Teniendo en cuenta que la ecuación de la recta que pasa por los puntos (a;f(a)) y (b;f(b)) es:
El área bajo esta línea recta en el intervalo [a;b] está dada por:
Esta integral constituye una aproximación de la integral de f(x) en dicho intervalo. El resultado de la integral anterior es:
que se denomina regla del trapecio.
Geométricamente, la regla del trapecio consiste en aproximar el área debajo de la curva definida por f(x), por el área bajo la recta que une los puntos (a, f(a)) y (b, f(b)). Recuerde que la fórmula para calcular el área de un trapecio es la altura por el promedio de las bases.
Cuando se emplea la integral bajo un segmento de línea recta para aproximar la integral bajo una curva, obviamente se tiene un error que puede ser importante. Una estimación del error de truncamiento E de la regla del trapecio es:
donde
ξ Є (a;b). La expresión anterior
indica que si la función a integrar es lineal, la regla del
trapecio será exacta. Es decir, la regla del trapecio tiene grado de
precisión n = 1. Además, sólo es posible aplicar la regla del
trapecio si f(x) es de clase C2[a;b].
Una forma de mejorar la precisión de la regla del trapecio consiste en dividir el intervalo de integración [a;b] en varios segmentos, y aplicar el método a cada uno de ellos. Las áreas de los segmentos se suman después para obtener una aproximación de la integral en todo el intervalo. Las expresiones resultantes se llaman fórmulas de integración, de aplicación múltiple o compuestas.
La siguiente figura muestra el formato general y la nomenclatura que se usará para obtener integrales de aplicación múltiple.
Si hay n+1 puntos igualmente espaciados, existen n segmentos del mismo ancho:
Si a y b se designan como x0 y xn, respectivamente, la integral completa se representará como:
Sustituyendo la regla del trapecio en cada integral se obtiene:
o, agrupando términos:
El error que se comete al aplicar la regla compuesta del trapecio está dado por:
Esto significa que el error es de orden O(h2). Además, cuando las derivadas de f(x) se conocen, es posible estimar el número de sub-intervalos necesarios para alcanzar la precisión deseada.
Método de Simpson 1/3
Los ingenieros encuentran con frecuencia el problema de integrar funciones que están definidas en forma tabular o en forma gráfica y no como funciones explícitas, se pueden utilizar métodos gráficos, pero los métodos numéricos son mucho mas precisos.
La integración numérica consiste en encontrar una buena aproximación al área bajo la curva que representa una función f(x), que ha sido determinada a partir de datos experimentales o a partir de una expresión matemática.
Las formulas de cuadratura de Newton-Cotes son los procedimientos mas comunes de integración numérica, se basan en la estrategia de reemplazar una función complicada o datos tabulados con una función aproximada que sea fácil de integrar, estas son:
- La regla de integración Trapezoidal.
- La regla de Simpson.
Estas reglas están diseñadas para casos en los que los datos a integrarse están espaciados de manera uniforme.
A continuación se describe la regla de integración de Simpson 1/3 para la “integración cerrada” es decir, para cuando los valores de la función en los extremos de los límites de integración son conocidos.
Además de aplicar la regla trapezoidal con segmentación mas fina, otra forma de obtener una estimación mas exacta de una integral es con el uso de polinomios de orden superior para conectar los puntos (en lugar de utilizar líneas para conectarlos).
Las reglas de Simpson son las fórmulas que resultan al tomar las integrales bajo los polinomios que conectan a los puntos.
El método de Integración Simpson 1/3 consiste en tomar el área bajo una parábola que conecta tres puntos, como se muestra en la siguiente gráfica:
Dada una función tabular con espaciamientos constantes, de la forma:
La fórmula de integración de Simpson 1/3 es la siguiente:
Método de Simpson 3/8
De manera similar a la obtención de la regla del trapecio y Simpson, es posible ajustar un polinomio de Lagrange de tercer grado a cuatro puntos e integrarlo:
para obtener:
donde h=(b-a)/3. Esta expresión se llama regla 3/8 de Simpson debido a que h se multiplica por 3/8. Ésta es la tercera fórmula de integración cerrada de Newton - Cotes.
Cuadratura de Gauss
El objetivo de la cuadratura de Gauss es determinar las abscisas x1 y x2 y dos coeficientes w1 y w2 de manera que la fórmula:
sea exacta para polinomios cúbicos de la
forma f(x) = a3x3 + a2x2 + a1x
+a0. Como hay que determinar cuatro números w1, w2,
x1 y x2 en la expresión anterior, se deben
seleccionar cuatro condiciones que deben cumplirse. Usando el hecho de
que la integración es aditiva, será suficiente con exigir que la
integral anterior sea exacta para las cuatro funciones f(x) = 1, x, x2,
x3. Por lo tanto, las cuatro condiciones de integración son:
De esta manera, el sistema de ecuaciones
no lineales que se debe resolver es:
Así, se ha encontrado los nodos y los coeficientes o pesos con los que se construye la cuadratura de Gauss. En consecuencia, si f es continua en [-1;1], resulta:
La cuadratura de Gauss con dos nodos G2(f) tiene grado de precisión n=3 y si f Є C4[-1;1], entonces,
siendo
para algún punto
ξ Є
[-1;1].
Diferenciación Numérica
Por definición la derivada de una función
 es:
es:Diferencias hacia adelante:
Diferencias centrales:
Bibliografía
http://www.frsn.utn.edu.ar/GIE/AN/IN/
http://www.frsn.utn.edu.ar/GIE/AN/IN/Formulas_Newton_Cotes.html
http://test.cua.uam.mx/MN/Methods/Integracion/Simpson13/Simpson13.php
http://www.frsn.utn.edu.ar/GIE/AN/IN/Cuadraturas_Gauss_Legendre.html



























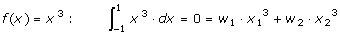











No hay comentarios.:
Publicar un comentario